Se define cada número complejo z como un par ordenado de
números reales: z = (a, b). A su vez el primer elemento a se define como parte
real de z, se denota a= Re(Z); el
segundo elemento b se define como parte imaginaria de z, se denota b=Lm(z).
Luego en el conjunto C de los números complejos, se definen tres operaciones y
la relación de igualdad:


Se define un número complejo especial, sobre todo en el álgebra, de suma
relevancia, el número i ( j en física), llamado unidad
imaginaria, definido como

Que satisface la siguiente igualdad:

De donde resulta:

Tomando en cuenta que  ,
cabe la identificación
,
cabe la identificación
 ,
cabe la identificación
,
cabe la identificación
Conjugado de un numero complejo
Dos binomios se llaman conjugados si solo difieren en su signo central, por
ejemplo, los dos binomios: 3m - 1 y 3m + 1 son conjugados.
El conjugado de un complejo z (denotado como 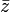 ó
ó 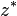 ) es un nuevo número
complejo, definido así:
) es un nuevo número
complejo, definido así:
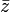 ó
ó 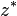 ) es un nuevo número
complejo, definido así:
) es un nuevo número
complejo, definido así:
Se observa que ambos difieren en el signo de la parte imaginaria.
Con este número se cumplen las propiedades:
Esta última fórmula es el método elegido para calcular el inverso de un
número complejo si viene dado en coordenadas rectangulares.
Un número complejo es igual a su conjugado si solo si es un número real.
Representación binó-mica

es la expresión binomial del punto.
Un número complejo se representa en forma binomial como:

La parte real del número complejo y la parte imaginaria, se pueden expresar
de varias maneras, como se muestra a continuación:

 ..
..



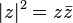
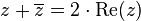

No hay comentarios.:
Publicar un comentario